program operasi matriks
Hai sahabat seperjuangan, seperti biasa di kesempatan kali ini saya ingin berbagi kepada anda semua mengenai program operasi Matriks. Nah di materi kita kali ini kalian akan memahami dan akan melihat bentuk-bentuk soal beserta pembahasannya yang berhubungan dengan matriks.
Sebelum kita masuk ke inti dasar dalam judul yaitu program operasi aritmatika, saya akan memperkanalkan diri, perkenalan nama saya Kunto Wicaksono Wibowo saya membuat blogger untuk menlengkapi tugas saya yang di berikan oleh dosen saya yang bernama Pak Ade dengan mata kuliah Ajabar Linear, saya kuliah di akademi telkom jakarta, saya akan lansung masuk ke inti nya agar tidak bertele tele lagi.
Matriks adalah sekumpulan bilangan yang disusun secara baris dan kolom dan ditempatkan pada kurung biasa atau kurung siku. Ordo suatu matriks adalah bilangan yang menunjukkan banyaknya baris (m) dan banyaknya kolom (n).
Penulisan matriks:

atau

Ordo suatu matriks adalah bilangan yang menunjukkan banyaknya baris (m) dan banyaknya kolom (n).
 Matriks di atas berordo 3x2.
Matriks di atas berordo 3x2.
Matriks Identitas (I)
Matriks identitas (I)adalah matriks yang nilai-nilai elemen pada diagonal utama selalu 1.

Matriks Transpose (At)
Matriks transpose adalah matriks yang mengalami pertukaran elemen dari baris menjadi kolom dan sebaliknya. Contoh:

maka matriks transposenya (At) adalah 
Operasi perhitungan pada matriks
Kesamaan 2 matriks
2 matriks dikatakan sama jika ordonya sama dan elemen yang seletak sama.
Contoh: 
Tentukan nilai 2x-y+5z!
Jawab:
 maka
maka 
 maka
maka 
 maka
maka 



Penjumlahan matriks
2 matriks bisa dijumlahkan jika ordonya sama dan penjumlahan dilakukan dengan cara menjumlahkan elemen yang seletak.
Contoh: 
Pengurangan matriks
2 matriks bisa dikurangkan jika ordonya sama dan pengurangan dilakukan dengan cara mengurangkan dari elemen yang seletak.
Contoh: 
Perkalian bilangan dengan matriks
Contoh:

Perkalian matriks
2 Matriks dapat dikalikan jika jumlah baris matriks A = jumlah kolom matriks B.
Penghitungan perkalian matriks:
Misalkan:
 dan
dan 
maka 
Contoh:

Determinan suatu matriks
Pengertian Determinan Matriks
Pertama kita pahami dulu apa sih Determinan Matriks itu, kurang lebih pengertiannya adalah sebagai berikut:
Determinan Matriks adalah sebuah angka atau skalar yang diperoleh dari elemen-elemen matriks tersebut dengan operasi tertentu. Determinan Matriks hanya dimiliki oleh matriks yang memiliki jumlah baris dan kolom yang sama atau disebut dengan matriks persegi.
Konsep Determinan Matriks
Setelah memahami 2 hal diatas tadi, selanjutnya kita lanjut ke konsep determinan matriks itu sendiri. Untuk tingkat SMA sendiri, yang akan dipelajari yaitu matriks ordo 2×2 dan ordo 3×3. Nah untk itu kita akan membahasnya satu persatu.
⇒ Matriks Ordo 2×2Nah untuk matriks ordo 2×2 ini masih sederhana, kita cukup memahami yang namanya diagonal utama dan diagonal samping untuk menyelesaikan soal determinan matriks 2×2 ini. Bagi kalian yang belum paham, silahkan kalian baca dulu mengenai pengertian dan jenis-jenis matriks.
Matriks ordo 2x2
Misalkan:

maka Determinan A (ditulis  ) adalah:
) adalah:

Matriks Ordo 3×3
Untuk determinan dari matriks ordo 3×3 ini sedikit rumit, namun konsepnya masih sama seperti ordo 2×2 tadi yaitu dengan cara mengurangkan diagonal utama dengan diagonal samping.
Matriks ordo 3x3
Cara Sarrus
Misalkan:
Jika  maka tentukan
maka tentukan  !
!

Penghitungan matriks dilakukan dengan cara menambahkan elemen dari kiri atas ke kanan bawah (mulai dari a → e → i, b → f → g, dan c → d → h) lalu dikurangi dengan elemen dari kanan atas ke kiri bawah (mulai dari c → e → g, a → f → h, dan b → d → i) sehingga menjadi:

Contoh:
 maka tentukan
maka tentukan  !
!


Cara ekspansi baris-kolom
Misalkan:
Jika  maka tentukan
maka tentukan  dengan ekspansi baris pertama!
dengan ekspansi baris pertama!


Seperti yang sudah ada diatas, kita harus menambahkan 3 baris dan 2 kolom disebelah kanan dari matriks A tersebut sehingga nantinya akan ketemu hasilnya. Untuk rumusnya sudah tertera pada gambar diatas.
⇒ Menyelesaikan SPLDV dengan DeterminanNah yang akan kita bahas selanjutnya yaitu cara menyelesaikan sebuah persamaan linear dua variabel menggunakan konsep determinan.
Yang perlu dipahami adalah Determinan Utama, Determinan Variabel x dan Determinan Variabel y.
- Determinan Utama (D) adalah determinan yang koefisiennya x dan y. Koefisien x masing-masing terletak pada kolom pertama, sedangkan koefisien y terletak masing-masing di kolom kedua.
- Determinan Variabel x (Dx) adalah determinan yang diperoleh dengan cara mengganti koefisien-koefisien variabel x dari determinan utama dengan bilangan-bilangan ruas kanan.
- Determinan Variabel y (Dy) adalah determinan yang diperoleh dengan cara mengganti koefisien-koefisien variabel y dari determinan utama dengan bilangan-bilangan ruas kanan
Matriks Singular
Matriks singular adalah matriks yang nilai determinannya 0.
Contoh:

Jika A matriks singular, tentukan nilai x!
Jawab:


 vs
vs 
Invers matriks
Invers matriks 2x2
Misalkan:

maka inversnya adalah:

Sifat-sifat invers matriks




Persamaan matriks
Tentukan X matriks dari persamaan:
- Jika diketahui matriks A.X=B




- Jika diketahui matriks X.A=B




Matriks – Operasi Matriks, Rumus, Contoh Soal Matriks dan Jawabannya Lengkap – Dalam matematika, matriks adalah susunan bilangan, simbol, atau ekspresi, yang disusun dalam baris dan kolom sehingga membentuk suatu bangun persegi.
Pemanfaatan matriks misalnya dalam menemukan solusi sistem persamaan linear. Penerapan lainnya adalah dalam transformasi linear, yaitu bentuk umum dari fungsi linear, misalnya rotasi dalam 3 dimensi.
Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Dimensi matriks dapat berupa 2 x 3 (dua baris dan tiga kolom), 3 x 2 (tiga baris dan dua kolom) , 3 x 3 (tiga baris dan tiga kolom) dan lain-lain.
Pada umumnya, matriks ditulis dalam tanda kurung siku atau kurung kurawal “[]”.
Operasi Dasar MatriksPenjumlahan dan Pengurangan Matriks
A + B = B + A
(A + B) + C = A + (B + C)
A – B ≠ B – A
Perkalian Matriks
Perkalian matriks dengan bilangan bulat dikombinasikan dengan penjumlahan atau pengurangan matriks bisa dilakukan pada matriks dengan ordo sama. Berikut sifat-sifat perkaliannya:
r(A – B) = rA – rB
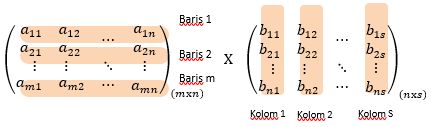
Elemen-elemen matriks C(mxs) merupakan penjumlahan dari hasil kali elemen-elemen baris ke-i matriks A dengan kolom ke-j matiks B. Berikut skemanya:
ABC = (AB)C = A(BC)
A(B + C) = AB + AC
(A + B)C = AC + BC
Determinan Matriks
3. Apabila suatu baris atau kolom determinan matriks memiliki faktor p, maka p bisa dikeluarkan menjadi pengali.
4. Apabila dua baris atau dua kolom merupakan saling berkelipatan, maka nilai determinannya adalah 0.
5. Nilai determinan dari matriks segitiga atas atau bawah adalah hasil kali dari elemen-elemen diagonal saja.
Invers Matriks
Berikut sifat-sifat invers matriks:
(A-1)-1 = A
(AB)-1 = B-1A-1Jika AX = B, maka X = A-1B
Jika XA=B, maka X = BA-1
Contoh Soal Matriks dan Pembahasan Matriks
Maka, tentukan A-B
A-B =
2. Perhatikan matriks P dan matriks Q, berikut ini.
4. Tentukan determinan dari matriks A berikut ini
Pembahasan:
det A = |A| = ad − bc = (5)(2) − (1)(−3) = 10 + 3 = 13
2b = 10 → b = 5
2x = 12 → x = 6
y = 6
y = 2
a + b + x + y = 3 + 5 + 6 + 2 = 16
Jawab:
Penjumlahan dan pengurangan matriks hanya bisa dilakukan jika kedua matriks memiliki ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.
Penjumlahan Matriks
-
Pengurangan Matriks
Sifat penjumlahan dan pengurangan matriks, diantaranya yaitu:
Matriks dapat dikalikan dengan bilangan bulat maupun dengan matriks lain. Setiap perkalian matriks, memiliki syarat masing-masing, diantaranya yaitu:
a. Perkalian Matriks Dengan Bilangan Bulat atau Perkalian Skalar Matriks
Matriks bisa dikalikan dengan bilangan bulat, maka hasil perkalian tersebut berupa matriks dengan elemen-elemennya yang merupakan hasil kali antara bilangan dan elemen-elemen matriks tersebut. Jika matriks A dikali dengan bilangan r, maka r.A =(r.aij). Contohnya:
r(A + B) = rA + rB
b. Perkalian Dua Matriks
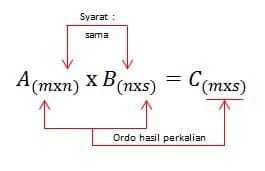
Perkalian antara dua matriks misalnya matriks A dan B, bisa dilakukan jika jumlah kolom A sama dengan jumlah baris B. Perkalian tersebut menghasilkan matriks dengan jumlah baris sama dengan matriks A dan jumlah saman dengan matriks B, sehingga:
Misalnya matriks A berordo (3 x 4) dan matriks B berordo (4 x 2), maka matriks C berordo (3 x 2). Elemen C pada baris ke-2 dan kolom ke-2 atau a22 diperoleh dari jumlah hasil perkalian elemen-elemen baris ke-2 matriks A dan kolom ke-2 matriks B. Contohnya:
Perlu diingat sifat perkalian dua matriks bahwa:
A x B ≠ B x A
Terbukti bahwa A x B ≠ B x A. Ada sifat-sifat lain perkalian matriks dengan bilangan atau dengan matriks lain, sebagai berikut:
k(AB) = (kA)B
Determinan dari matriks A diberi notasi tanda kurung, sehingga penulisannya |A|. Determinan hanya bisa dilakukan pada matriks persegi.
Determinan matriks ordo 2×2
Determinan matriks ordo 3×3 (aturan Sarrus)
Berikut sifat-sifat determinan matriks:
1. Determinan A = Determinan AT
2. Tanda determinan berubah jika 2 baris/2 kolom yang berdekatan dalam matriks ditukar.
Suatu matriks A memiliki invers (kebalikan) jika ada matriks B yang dapat membentuk persamaan AB = BA = I, dengan I adalah matriks identitas. Invers dari suatu matriks berordo (2 x 2) seperti 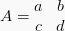 bisa dirumuskan sebagai:
bisa dirumuskan sebagai:
AA-1 = A-1A = I
1. Dua buah matriks A dan B masing-masing berturut-turut:
Pembahasan:
Tentukan matriks PQ
Pembahasan:
3. Dari dua buah matriks di bawah ini:
Tentukan 2A + B
Pembahasan:
5. Tentukan nilai a + b + x + y dari matriks berikut ini:
Diketahui bahwa P = Q
Pembahasan:
3a = 9 → a = 3
Sehingga:
6. Tentukan tranpose dari matriks A berikut ini:
7. Tentukan invers dari matriks berikut ini:
Pembahasan:
Demikian penjelasan yang bisa kami sampaikan tentang Matriks – Operasi Matriks, Rumus, Contoh Soal Matriks dan Jawabannya Lengkap . Semoga bermanfaat dan sampai jumpa pada postingan selanjutnya.
sumber:
- http://www.catatanrobert.com/operasi-aritmatika-matriks/
https://id.wikibooks.org/wiki/Subjek:Matematika/Materi:Matriks
https://www.studiobelajar.com/matriks-perkalian-determinan-invers/
https://nanyajawab.com/determinan-matriks-pembahasan-contoh-soal/
https://www.pelajaran.co.id/2018/06/operasi-matriks-rumus-contoh-soal-matriks-dan-jawabannya.html
https://id.wikipedia.org/wiki/Matriks_(matematika)





















































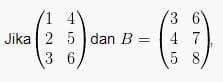
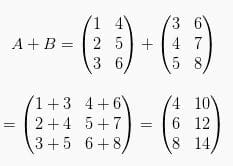
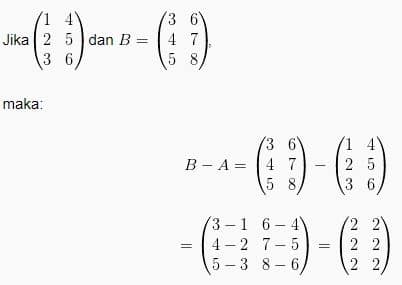
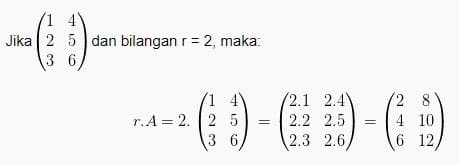

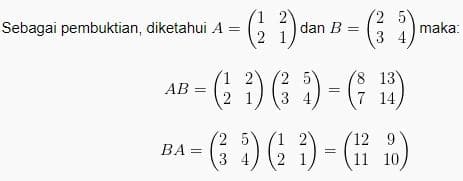
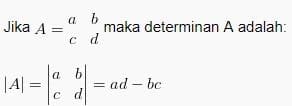

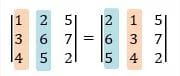
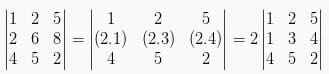
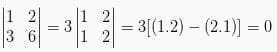
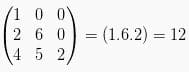
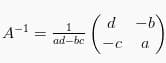
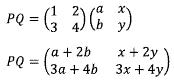
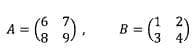
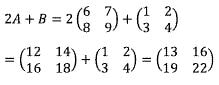
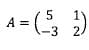
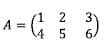
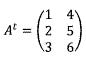
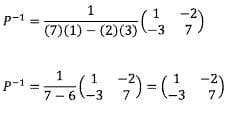
Komentar
Posting Komentar