PENGOPRASIAN BILANGAN DETERMINAN MATRIKS
Disini saya akan menjelaskan tentang pengoperasian bilangan determinan matriks, mungkin langsung saja ketahap selanjutnya.
Pengertian determinan matriks.
Matriks adalaha bidang materi aljabar linear, determinan ialah sebuah nilai yang dapat dihitung dari suatu matriks persegi.
Determinan matriks A ditulis dengan sebuah tanda, yaitu: det(A), det A atau │A│.
Determinan bisa dianggap sebagai factor penskalaan transformasi yang di gambarkan oleh matriks.
Determinan Matriks Ordo 2 x 2
Seperti yang sobat idschool sudah ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.
Nilai determinan A disimbolkan dengan  , cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
Determinan Matriks Ordo 3 x 3
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.
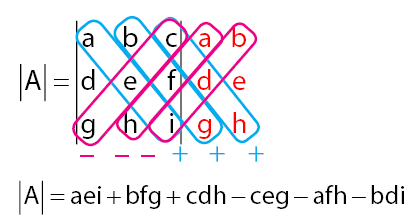
Contoh soal determinan matriks ordo (2x2)
1. A = 5 3
8 -7
8 -7
Berapakah nilai │A│adalah
A = 5 3
8 -7
8 -7
│A│ = ad-bc
│A│ = 5.(-7) – 8.3
│A│ = -59
Contoh soal determinan matriks ordo (3x3)
1. X = 7 6 8
9 7 4
2 0 -3
9 7 4
2 0 -3
Berapakah nilai │X│?
│X│=
9 7 4 9 7
2 0 -3 2 0
2 0 -3 2 0
= (7.7.-3) + (6.4.2) + (8.9.0) – (6.9.-3) – (7.4.0) – (8.7.2)
= (-149 + 48 +0) – (-162 + 0 –112)
= -99 - (-228)
= 129
Terima kasih, yuk kunjungi jugaKampus kami
BalasHapusTerima Kasih atas informasinya.
BalasHapusBelajar Website Developer
Klik Disini